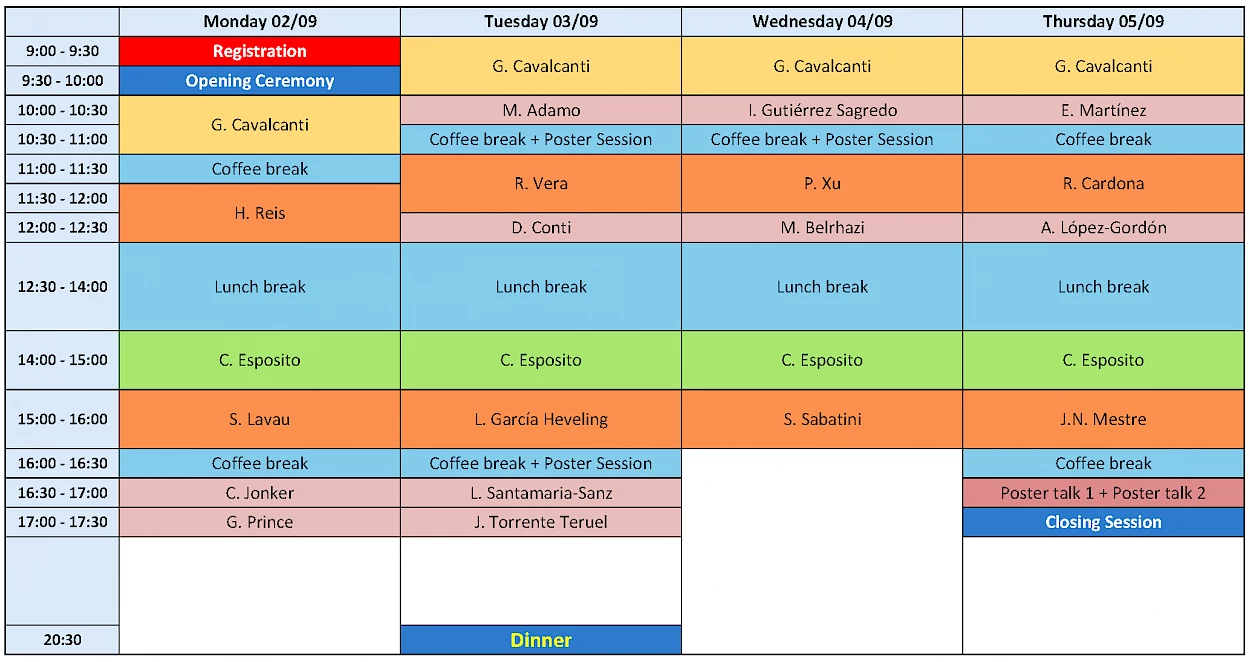
Programme
Book of abstracts
Mini-courses
University of Salerno, Italy
Reduction theory
This minicourse will focus on the theory of reduction from different points of view. Poisson manifolds occur as phase spaces in classical mechanics and there the presence of symmetries allows us, under suitable assumptions, to reduce the phase space associated with a dynamical system. We will start with the classical theorem of Marsden and Weinstein on phase space reduction in the case of symplectic or more general Poisson manifolds. As a second step we will try to rephrase reduction in algebraic terms. Finally, we will introduce coisotropic reduction and reinterpret the Marsden-Weinstein reduction as a special case.
Utrecht University, The Netherlands
The geometry and topology of T-duality
T-duality is a relation between spaces that originated in String Theory. Physically string compactifications on T-dual spaces describe the same physics. In this course we will take a mathematical approach to T-duality. We will introduce different mathematical formulations of T-duality, highlighting their similarities and differences and relations between T-dual spaces.
Topics we aim to cover include:
- T-duality for principal circle and torus bundles,
- Topological T-duality,
- T-duality and Courant algebroids,
- T-duality of heterotic Courant Algebroids,
- T-duality for torus actions with fixed points,
- Poisson—Lie duality
- Spherical T-duality.
Invited talks
University of Porto, Portugal
Construction of algebraic vector fields out of projective structures
Given a singular uniformizable projective structure on CP(1), we will show how to associate it with a rational vector field with univalued solutions.
This is a joint work with A. Elshafei and J. Rebelo.
University of Coimbra, Portugal
Multiplicative tensors - a cohomological point of view
Multiplicative tensors are sections of tensors products (possibly symmetric, or exterior) of vector bundles, which are compatible with a multiplication - for example that of a Lie group or Lie groupoid. Some examples are multiplicative differential forms, multiplicative multivector fields, and multiplicative complex structures on Lie groupoids.
We will describe a cohomology for tensor powers of vector bundles over Lie groupoids, for which multiplicative tensors arise as cocycles. We will then describe some properties of this cohomology, as well as applications to deformation theory of holomorphic Lie groupoids.
This is joint work with Lennart Obster and Luca Vitagliano
University of Hamburg, Germany
Causal boundaries and spacetime splitting
In geometry, one often wishes to add a boundary to a space consisting of the "points at infinity". For the spacetimes of general relativity, this is accomplished by the causal boundary. In this talk, after introducing the relevant concepts, we will discuss how understanding the causal boundary leads to progress on Bartnik's splitting conjecture. The latter states that certain spacetimes split isometrically into a product Lorentzian manifold, and is related to the question of rigidity of the celebrated Hawking-Penrose singularity theorem.
Penn State University, USA
$BV_\infty$ quantization of (-1)-shifted derived Poisson manifolds
In this talk, we will give an overview of (-1)-shifted derived Poisson manifolds in the $C^\infty$-context, and discuss the quantization problem. We describe the obstruction theory and prove that the linear (-1)-shifted derived Poisson manifold associated to any $L_\infty$-algebroid admits a canonical $BV_\infty$ quantization.
This is a joint work with Kai Behrend and Matt Peddie.
University of the Basque Country, Spain
New characterization of the Robertson-Walker geometry
The basis for the standard model in Cosmology is the Robertson-Walker (RW) spacetime. The geometric nature of gravity makes the geometric characterization of spacetimes of great importance. The characterizations of the RW geometry involve several kinds of ingredients with different geometrical/physical/observational weight, and different characterizations probe different aspects the theory. The aim of this work is two-fold. We establish a novel geometric characterization of the RW spacetime, involving an arbitrary single observer and, along the process, we find a canonical form of the RW metric associated to any such single observer equipped with an arbitrary space frame.
University of Barcelona, Spain
Contact topology and time-dependent hydrodynamics
More than twenty years ago, Etnyre and Ghrist established a connection between contact topology and a class of stationary solutions to the 3D Euler equations for ideal fluids. In this talk, we present a new framework that allows assigning contact/symplectic invariants to large sets of time-dependent solutions to the Euler equations on any three-manifold with an arbitrary fixed Riemannian metric, thus broadening the scope of contact topological methods in hydrodynamics. We use it to prove a very general non-mixing result for the infinite-dimensional dynamical system defined by the equation and to show the existence of new conserved quantities obtained from Floer theories in contact topology.
This is joint work with Francisco Torres de Lizaur.
University of Cologne, Germany
Positive monotone symplectic manifolds with symmetries
Positive monotone symplectic manifolds are the symplectic analogues of Fano varieties, namely they are compact symplectic manifolds for which the first Chern class equals the cohomology class of the symplectic form.
In dimension 6, if the positive monotone symplectic manifold is acted on by a circle in a Hamiltonian way, a conjecture of Fine and Panov asserts that it is diffeomorphic to a Fano variety.
In this talk I will report on recent classification results of positive monotone symplectic manifolds endowed with some special Hamiltonian actions of a torus, showing some evidence that they are indeed (homotopy equivalent/homeomorphic/diffeomorphic to) Fano varieties.
Galatasaray Üniversitesi, Turkey
A graded geometric perspective on tensor hierarchies
Tensor hierarchies, as they emerge in gauged supergravity, are differential graded Lie algebras with specific properties. This implies that the space of differential forms taking values in a tensor hierarchy algebra (THA) is also a differential graded Lie algebra L, of which the embedding tensor is a Maurer-Cartan element. Whenever one makes a gauge transformation of the latter, one obtains a homological derivation on the space of forms valued in the THA. In the graded geometric language, this makes L a differential graded Lie algebroid. All relevant physical objects -- the gauge fields, the field strengths, the gauge transformations and their commutator -- then inherit a very simple graded geometric interpretation. This opens the possibility of unifying many gauge theories (Yang-Mills, Leibniz,...) under one unique formalism. Moreover, the L_infinity algebras associated to such theories are readily obtained from the differential graded Lie algebra by a very simple procedure. The talk will be an overview of some mathematical properties of tensor hierarchy algebras, and of their graded geometric interpretation.
(in collaboration with Thomas Basile, Mons)
Contributed talks
ICMAT-CSIC, Spain
Contact bi-Hamiltonian systems
Magri and his collaborators investigated the connection between bi-Hamiltonian manifolds (manifolds M equipped with two Poisson structures that satisfy a mutual compatibility condition) and integrable systems. Specifically, when one of the Poisson structures is invertible (originating from a symplectic structure), it allows for the definition of an endomorphism N on the tangent space TM of the manifold M by composing one Poisson structure with the inverse of the other. In this context, the absence of the Nijenhuis torsion of N is both a necessary and sufficient condition for the compatibility of the two Poisson structures. This concept has been extended to Jacobi manifolds by Marrero et al. and Nunes da Costa. It is important to note that contact manifolds are specific instances of Jacobi manifolds. In fact, every Jacobi manifold is foliated into leaves that are either contact or locally conformally symplectic manifolds. In this presentation, I will discuss some findings from ongoing research on the relationship between Jacobi–Nijenhuis structures and the integrability of contact Hamiltonian systems.
University of Toronto, Canada
Graded symplectic geometry and generalized Kähler-Ricci flow
Bi-Hermitian geometry, initally discovered by physicists in their investigation of supersymmetric string theory, was later rediscovered by Gualtieri as part of Hitchin's generalized geometry program. This discovery unearthed many beautiful connections to Poisson and Dirac geometry. One of these that has only recently begun to be investigated is the connection between bi-Hermitian manifolds (also known as generalized Kähler manifolds) to graded symplectic geometry. I will give an overview of these developments. In particular, I will explain how the generalized Kähler-Ricci flow, which also has origins in string theory, can be described as the flow by a Hamiltonian vector field on a graded symplectic manifold.
University of Pisa, Italy
Invariant Einstein metrics and special geometries
The interplay between the Einstein equation ric = λg and special geometries is a classical object of study in Riemannian geometry, whose main ramifications are Kähler-Einstein, Sasaki-Einstein and special holonomy metrics. In particular, among Einstein metrics, those admitting a parallel or Killing spinor are of special interest.
Another aspect of Einstein metrics concerns the study of symmetries, and in particular homogeneous metrics. It is now known by results of Heber, Lauret, Jablonski and Böhm- Lafuente that homogeneous Einstein metrics of negative curvature can be described in terms of solvable Lie algebras with an orthogonal splitting n ⋊ a, with n nilpotent and a abelian acting by symmetric derivations on n.
The two points of view have little intersection, as the existence of a Killing or parallel spinor on a solvmanifold forces the geometry to be trivial.
In this talk I will discuss the extent to which these ideas, constructions and obstructions generalize to indefinite metrics. I will show how one can construct vast classes of indefinite Einstein solvmanifolds with a splitting n ⋊ a as outlined above and explain that pseudo-Kähler-Einstein metrics may arise in this way, but not special geometries defined by a Killing spinor, and whilst indefinite Einstein solvmanifolds with a Killing spinor do exist, they require a different construction.
This talk is based on joint work with Federico A. Rossi and Romeo Segnan Dalmasso.
University of Zaragoza, Spain
Sundman transformations and linearization of second-order differential equations
Sundman transformations are infinitesimal time reparametrisations. They transform a differential equation into another differential equation, whose solutions are reparametrisation of the solutions of the first equation. Therefore, they provide an important method to integrate, or to simplify, a given differential equation.
Our main interest is in the case of a second-order differential equation (SODE). A Sundman transformation defined by a basic function transforms a SODE into a new SODE but with respect to a modified tangent structure. Consequently, all the geometric objects associated to a SODE are also modified or transformed.
By using this geometric objects we will consider the problem of linearizability of second order differential equations, that is, the existence of a Sundman transformation and a coordinate system in which the transformed SODE is linear.
La Trobe University, Australia
Covariant derivatives for Ehresmann connections
Covariant derivatives are constructed for a broad class of Ehresmann connections on fibre bundles.
A vertical endomorphism allows construction of covariant derivatives separately on both the vertical and horizontal distributions of the connection which can then be non-trivially glued together on the total space.
A familiar tangent bundle connection illustrates the development.
This is joint work with David Saunders.
University of Burgos, Spain
Unimodularity and preservation of volume forms on Poisson-Lie groups and Poisson homogeneous spaces
In this talk I will present some recent results regarding the unimodularity of Poisson-Lie groups and Poisson homogeneous spaces, and its relation with the existence of certain volume forms for Hamiltonian systems.
In particular, for Poisson-Lie groups, I will show that Hamiltonian vector fields on a Lie group endowed with a unimodular Poisson-Lie structure preserve a multiple of any left-invariant volume on the group. Conversely, if there exists a Hamiltonian function such that the identity element of the Lie group is a nondegenerate singularity and the associated Hamiltonian vector field preserves a volume form, then the Poisson-Lie structure is necessarily unimodular.
In the case of Poisson homogeneous spaces, I will show that the unimodularity condition is much more restrictive. In order to do that I will introduce the notions of semi-invariant volume forms on homogeneous spaces, horizontal modular class and multiplicative unimodularity. These allow us to give infinitesimal conditions analogous to the Poisson-Lie group case. In addition, I will give necessary and sufficient conditions for a Hamiltonian vector field
to preserve an arbitrary volume form on a Poisson homogenous space. I will illustrate all these results with examples.
This is joint work with D. Iglesias Ponte, J. C. Marrero, E. Padrón and Z. Ravanpak.
University of Córdoba, Spain
New geometrical models in Newton-Cartan gravity
Since its geometric formulation by E. Cartan in the 1930s, Newton-Cartan theory has been a subject of significant interest within the mathematical physics research community. For instance, it was demonstrated to be a limit of General Relativity and constitutes a covariant formulation of Newtonian gravity. The Newton-Cartan framework is set in the context of Galilean spacetimes (M, Ω, g, ∇), where Mn+1 is a smooth manifold, Ω is a non-vanishing 1- form on M, g is a positive definite metric on the annihilator of Ω and ∇ is an affine connection compatible with Ω and g.
Novel geometrical models within this framework are the so-called Galilean Twisted Space-times, where Galilean Generalized Robertson-Walker Spacetimes arise as a particular case. They are defined as (I × F, dπI, f2πF∗ h|An(dπI), ∇), for an interval I, a Riemannian manifold (F, h) and a positive smooth function f ∈ C∞(I × F). The Galilean connection ∇ is the unique one such that ∂t =∂/∂πI is a geodesic and irrotational field of observers.
Some natural conditions are given to prove the completeness of free falling observers, that is, for the trajectories of particles to not vanish in a finite proper time. Moreover, global geometric conditions allow us to ensure the splitting of a Galilean spacetime into a Galilean Twisted Spacetime.
University of Burgos, Spain
Doubly special relativity as a non-local quantum field theory
In recent decades, the formulation of a quantum theory of gravity that unifies quantum field theory (QFT) and general relativity has been sought. Among all effective theories of quantum gravity describing some quantum effects at low-energy, doubly/deformed special relativity (DSR) deforms the kinematics of special relativity by introducing a high-energy scale while keeping a relativity principle. In this talk we formulate a DSR QFT in position
space, from a geometric point of view. Due to the infinite number of derivatives involved, this proposal leads to a non-local QFT that can be used simultaneously in string theory, causal set theory, and, for the first time, in DSR. We describe how to modify the usual QFT’s axioms in order to take into account the deformed symmetries of DSR. We also explain how the Klein–Gordon, Dirac, and electromagnetic Lagrangians are modified. For the latter, and considering a particular metric found to be privileged from a geometrical approach to DSR, we find that the electric potential of either a point charge and a magnetic dipole do not diverge at the origin only for AdS space, diverging for dS.
University of Antwerp, Belgium
Geodesic extensions of mechanical systems with nonholonomic constraints
For a Lagrangian system with nonholonomic constraints (L,D), the equations of motion follow from the so-called Lagrange-d’Alembert principle. It is well-known that this is not a purely variational principle (for the Lagrangian functional associated to L), since it only makes use of variations that are required to follow the constraints. The resulting equations, the so-called Lagrange-d’Alembert equations, are therefore not simply the Euler-Lagrange equations of L. In this talk we will construct extensions of these equations of motion to sets of second-order ordinary differential equations. This is what we will call a SODE extension.
In the case of a purely kinetic Lagrangian, we will derive the conditions under which the solutions of the Lagrange-d’Alembert equations are geodesics of a Riemannian metric, while preserving the constrained Lagrangian. We call this a geodesic extension. We interpret the algebraic and PDE conditions of this problem as infinitesimal versions of the relation between the nonholonomic exponential map and the Riemannian metric.
We discuss the special case of a Chaplygin system with symmetries and we end the talk with a worked-out example.
University of Burgos, Spain
Noncommutative Lightcones from Quantum Conformal Groups
Quantum Field Theory (QFT) on noncommutative spacetimes, initially proposed in 1947, aimed to resolve ultraviolet divergences in quantum electrodynamics. Renewed interest arose from quantum gravity’s limitations at the Planck scale, suggesting new spacetime models. Advances in the 1970s-80s led to noncommutative formulations of geometry and topology, enabling QFT on noncommutative spaces. Quantum groups, as noncommutative Lie groups, are crucial for describing symmetries in these spaces.
A key issue is causality, as weakened locality in noncommutative spacetimes can unpredictably affect it. This talk explores noncommutative lightcones in three-dimensional spacetime as quantum homogeneous spaces of a quantum group. Focusing on Poisson–Lie structures on the Lorentz group of 2+1-dimensional Minkowski spacetime, SO(2,1), we ensure noncommutative coordinates without involving external ones. The lightcone, a homogeneous space of SO(2,1), is formed by quotienting by the isotropy subgroup of a lightlike vector. Using 1990s Poisson–Lie structures, categorized by classical r-matrices [3], we define non-commutative structures.
Each Poisson–Lie family results in a Poisson homogeneous space on the lightcone due to coisotropy with respect to the isotropy subgroup, with one family leading to a Poisson homogeneous space of Poisson-subgroup type. This talk concludes by discussing the quantized homogeneous spaces derived from these structures and the implications for localization in noncommutative geometries.