Mathematical Analysis of Piezoelectric Problems

Problem Description

Piezoelectricity can be defined as an interaction between two phenomena: the direct piezoelectric effect (a mechanical deformation generates an electric field in the material) and the inverse piezoelectric effect (the application to the material of an electric field or of a potential difference generates a deformation), cf. T. Ikeda, Fundamentals of Piezoelectricity, Oxford University Press, Oxford, 1990. Therefore, a single piezoelectric device is both an actuator and a sensor, and consequently, piezoelectric materials belong to a class of smart or intelligent materials, that are very important in many applications as, for example, biomechanics, biomedicine, structural mechanics, etc.

Modelling & Computational Challenges

The scope of this project is essentially to acquire a better mathematical knowledge of some particular piezoelectric models, as adaptive rod models and composite laminated plate models. This research project will lead to a better understanding of the mechanical and electric behavior of these problems and, consequently, to an improvement of real-life applications.

Research at LCM

Research will be developed along the following lines:

• Asymptotic and variational methods for the mathematical formulation, and related questions of existence and regularity of solutions.

• Discretization schemes, using finite element and finite difference methods.

• Analysis of error estimates.

• Algorithms to solve the discrete problems, such as deterministic optimization algorithms and evolutionary algorithms.

• Code development (envolving both finite elements and optimization).

		
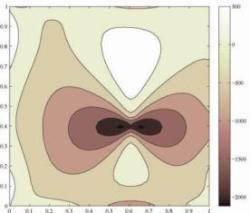
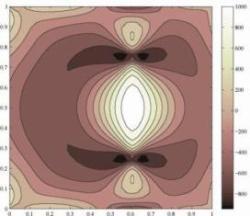
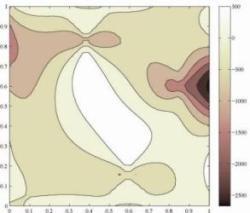
Contour plots of the electric potential for a square piezoelectric plate in frictional contact with a rigid obstacle (three different obstacles).

Papers & Reports

• [1] I. Figueiredo and G. Stadler, Frictional contact of an anisotropic piezoelectric plate, Preprint 07-16 of the Department of Mathematics, University of Coimbra, 2007
• [2] Georg Stadler, Elliptic optimal control problems with L1-control cost and applications for the placement of control devices, Preprint 06-42 of the Department of Mathematics, University of Coimbra, 2006
• [3] L. Costa, I. Figueiredo, R. Leal, P. Oliveira, G. Stadler, Modeling and numerical study of actuator and sensor effects for a laminated piezoelectric plate, Computers and Structures,  85(7-8) (2007) 385-403
• [4] Isabel N. Figueiredo and Georg Stadler, Optimal control of piezoelectric anisotropic plates, in  CD-ROM Proceedings of the III European Conference on Computational Mechanics: Solids, Structures and Coupled Problems in Engineering, C. A. Mota Soares et al. (eds.), Lisbon, Portugal, 5-8 June 2006
• [5] Isabel M. N. Figueiredo and Carlos M. F. Leal, A generalized piezoelectric Bernoulli-Navier anisotropic rod model, Journal of Elasticity,  85(2) (2006) 85-106
• [6] L. Costa, P. Oliveira, I.N. Figueiredo and R. Leal, Actuator effect of a piezoelectric anisotropic plate model, Mechanics of Advanced Materials and Structures, 13(5) (2006) 403-417.
• [7] Isabel N. Figueiredo, Approximation of bone remodeling models, Journal de Mathématiques Pures et Appliquées Vol. 84, 12 (2005) 1794-1812
• [8] Isabel N. Figueiredo; Carlos F. Leal and Cecília S. Pinto, Shape analysis of an adaptive elastic rod model, SIAM Journal on Applied Mathematics 66(1) (2005) 153-173
• [9] Isabel N. Figueiredo; Carlos F. Leal and Cecília S. Pinto, Conical differentiability for bone remodeling contact rod models, ESAIM: Control, Optimisation and Calculus of Variations, 11(3) (2005) 382-400
• [10] Isabel N. Figueiredo and Carlos F. Leal, A piezoelectric anisotropic plate model, Asymptotic Analysis, 44(3-4) (2005) 327-346

Software

• [1] Patches - Finite Element Code for Elastic Plates with Piezoelectric Patches (Matlab code for the software COMSOL MULTIPHYSICS 3.3) - available under request.
• [2] Lampiezo.m - Finite Element Code for a Laminated Piezoelectric Plate (Matlab code for the MATLAB Toolbox CALFEM) - available under request.
• [3] Piezo.m - Finite Element Code for a Piezoelectric Plate (MATLAB code for the Matlab Toolbox CALFEM) - available under request.

Project Team

• Isabel Maria Narra de Figueiredo, LCM/CMUC
• Carlos M. Franco Leal, LCM/CMUC
• Pedro N. F. P. Oliveira, Department of Production and Systems, University of Minho
• Rogério A. C. P. Leal, Department of Mechanical Engineering, University of Coimbra
• Georg Stadler, ICES, University of Texas at Austin, USA
• José António Carvalho, Department of Mathematics, University of Coimbra
• Lino Costa, Department of Production and Systems, University of Minho
• Cecília S. Pinto, Department of Mathematics, IPV
• Luis M. F. Roseiro, Department of Mechanical Engineering, ISEC
• Urbano M. O. Ramos, Department of Mechanical Engineering, ISEC

Project Reference

FCT Research Project - POCI/MAT/59502/2004